
(圖/shutterstock)
某餐廳牆上的壁畫 ~ 陳金瑩
數學顧名思義
是起源於「研究」「數」的學問
早年我們在學校
會先學分辨 自然數、整數、有理數、實數 ... 這些東東
再到學習 解方程式、向量、幾何 ...
但我想,除了對數學特別有興趣的讀者以外
恐怕對多數人來說
早就通通忘光了 @@
甚至只記得,快要考試了,數學都不太會的恐懼
坦白說,跟以前那些對數學特別有天份的同學相比
我不算一個數學特別好的人
但後來出社會工作
再到做自己的投資
我發現「數學貴為科學之母」這句話
真的不是老師在唬人
數學,
不只在人類各種學問中
都產了巨大的影響
在投資的世界,也完全不例外
以前在教科書上,看過去覺得很醜
只想考完試就把它忘光的方程式
原來,對於做投資
有非常大的「實戰」用途
所以這篇文章
我要來介紹幾個投資上用的到的數學觀念
已經忘光,或從來沒搞懂的投資朋友
注意囉 ...!
( 歡迎加入 ►► 凱旋投資術 FB 社團 )
1. 數學在投資上的主要用途
有別於純理論的數學研究
在數學家的世界裡,
還有將這些理論,擴展為各種不同分支的「應用數學」
包含 作業研究、控制理論,甚至生物數學 ... 等學科
這些應用數學當中,
與投資最相關的,非「統計學」莫屬!
統計學,
是一套研究如何 收集、偵測、歸納 ... 真實資料的學問
早年我自己在學數學的時候,其實對它並不是那麼有興趣
但後來學到統計學
由於開始接觸到真實資料
使我理解,原來這些東西都是有用的
都是可以拿來實戰的
尤其在到後面,數學並不再是「固定不變」
而是會跟隨某種既有規律但又十分不確定的「機率」而變動
「統計學」 + 「機率」 + 「真實資料」
讓我對這些事情,突然非常有興趣起來
也靠著這些方法
開發出自己獨有的投資模組。
2. 判別數值的大小與好壞
— 百分比臨界值 ( Percentile )
接著讓我來依序介紹
幾招在投資上很有用的數學觀念與方法
首先在投資的世界
由於我們經常需要接觸與分析許多數據資訊
比如,某某公司公布營收囉!
上個月年成長 10%
但這個成長 10%
到底是好或不好呢?
從絕對數值,我們並不一定能判別出數字的好壞
此時,我們可以善用「數學方法」中的「百分比臨界值」
把所有公司的營收數據,通通拿來做比較
便能客觀判定,這家公司的營收到底好不好
百分比臨界值,雖然讀起來有點文謅謅
但它本質上只是一種「排序看大小」的觀念而已
假設你取得了台股 1600 檔公司的營收年增率
把這些數值,從小排到大
再依序抽取出你想要的臨界值來製表
就能立刻判別出數值的大小與好壞
而且這個方法,只要善用 EXCEL 裡的 Percentile 函數
每個人都能靠自己,輕易做到喔!
下圖我以「台指選擇權市場」的波動率「真實資料」
實際貼一張圖給您看
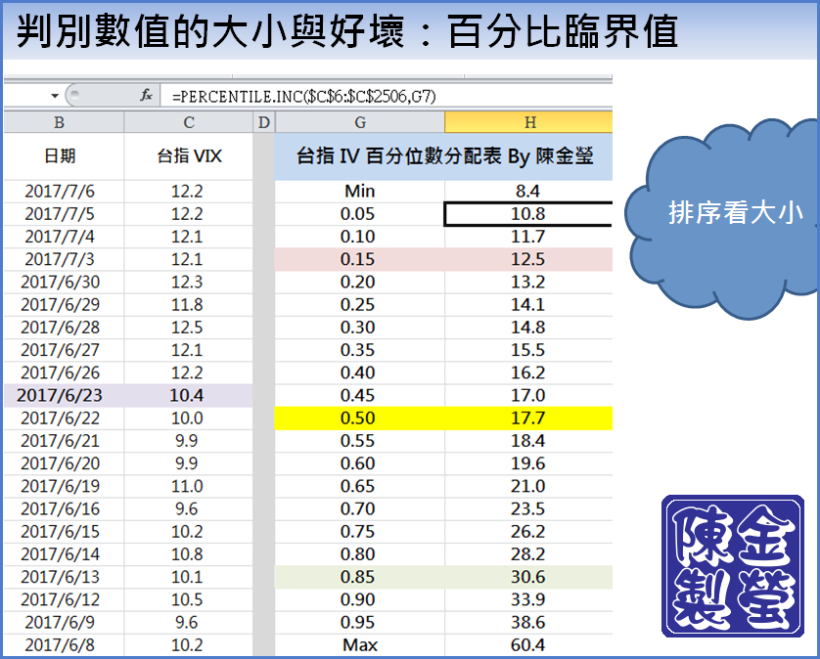
資料來源:陳金瑩
當你取得一串數列後
只要對著這串數列下 Percentile ( 資料區間,臨界值 ) 函數
EXCEL 就會幫你抽取出整串數列裡的對應數值
舉例來說,
當我對著過去十年的台指選擇權波動率資料
輸入抓取 0.05 ( 5% ) 臨界值的指令後
EXCEL 會傳回 10.8 這個數字
表示在過去十年中
台股每 100 個交易日
只有 5 天,波動率會落在 10.8 以下
其他 95 天都落在 10.8 以上
而當我輸入 Percentile ( 資料區間,臨界值 = 0.95 )
EXCEL 會傳回 38.6
表示在過去十年中
台股每 100 個交易日
只有 5 天,波動率會在 38.6 以上
3. 平均數與中位數
如果我們想要有一個快速理解一串數列的方法
那就莫非 平均數 或 中位數 莫屬
平均數的公式很簡單:把所有值加起來,除上你有幾筆資料
而中位數的公式則為:把所有值從大到小排序,取中間那一個
我們來看一下,以下兩組數列

兩組人馬,您覺得哪一組的年齡較大呢?
其實呢!
兩組人馬的平均年齡,一樣都是 14 歲
若從平均數的角度來看,你可以說他們一樣大
但仔細查看人馬 B
咦!
雖然算起來的平均數為 14
但七個人當中,竟然只有一個人 > 14 歲
其餘六個人,通通小於 14 歲
但若從「中位數」的角度來看
人馬 A 的中位數為 14
人馬 B 的中位數則為 5 ( 平均數為 14 )
5 這個數字,雖然會遺漏 72 這筆數值資訊
但比較能代表整串數列的表現
其實從理論上來說
平均數是一個很完美的指標
但它比較容易受到極端值的影響
由於金融市場,處處都充滿著極端值
所以如果我們只能以一個數字,來代表群體
我通常都是用「中位數」比較多
中位數與剛剛的百分比臨界值
同樣都可以用 EXCEL 一秒算出來
其公式為 median ( )
或者,若您充分理解 Percentile 這個函數的用法
Percentile ( 資料區間,臨界值 = 0.5 )
其實正好就是中位數的意思喔!
4. 充分條件與必要條件
老實說,我不太確定這兩個東東算不算數學
但由於它們是在邏輯上,非常重要的觀念
所以我一起講一下

畫的圖來看看,可以加強我們的理解
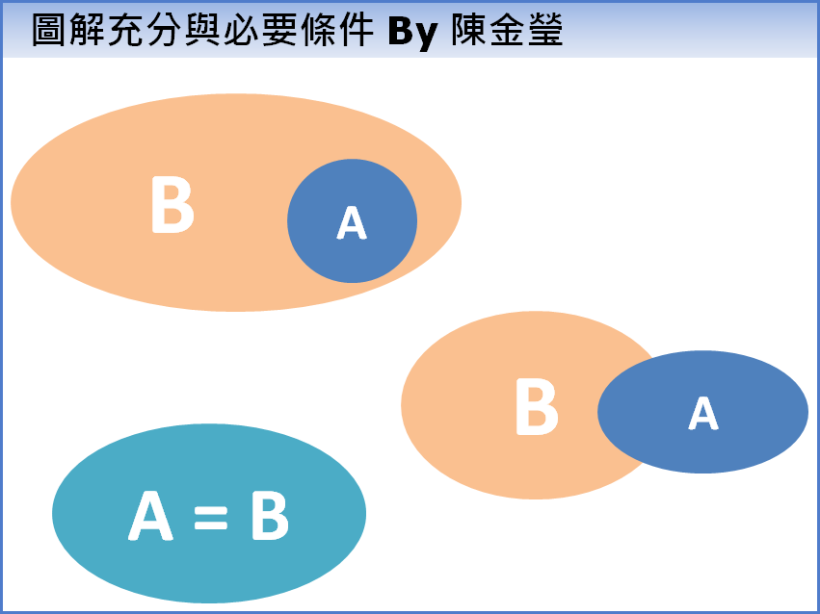
資料來源:陳金瑩
以上圖 左上 那個圖來說,
由於 A 發生了,就保證 B 一定也發生,故 A 是 B 的充分條件
而 A 如果要發生,必定要建立在 B 已經先發生,故 B 是 A 的必要條件
以上圖 左下 那個圖來說,
由於 A 與 B 幾乎是同樣的事情
例如:今天買到隔天會漲超過交易成本的股票 vs 隔天在這檔股票能否賺錢
故兩者互為充分與必要條件
以上圖 右邊 那個圖來說,
由於 A 與 B 互相無法確保另一件事會發生
所以兩者互相不是對方的充分或必要條件
5. 搞懂機率,投資不買錯

資料來源:陳金瑩
機率的概念,在投資的世界
是一門很重要的學問!
其實投資往往在玩的就是一種機率
比如說:買到一檔營收月月成長、法人天天買超、股價也不會很貴 的股票
會不會賺錢?
從機率的角度來講,當然是高的!
但很多投資朋友,
用了這樣「對的投資方法」 ( 從事前來看 )
試了一次,卻沒賺錢以後 ( 從事後來看 )
就開始摒棄這些「正統的」「高勝算投資方法」
而走上一些旁門走道
真的很可惜!
其實,你只要用同樣的方法,多試幾次
或者不要一次只買一檔股票
而是一次買 5 ~ 10 檔這樣的股票
只要方法是對的 ( 有比較高的機率能獲勝 )
累積下來的結果,就能反映到您的損益上
6. 明天的 1 元,不等於今天的 1 元
— 複利與折現
在投資的世界,還有一個非常重要的觀念:複利與折現
假設你期初以 100 萬進場投資,每年報酬率 10%
那麼持續十年之後,本金會變多少呢?
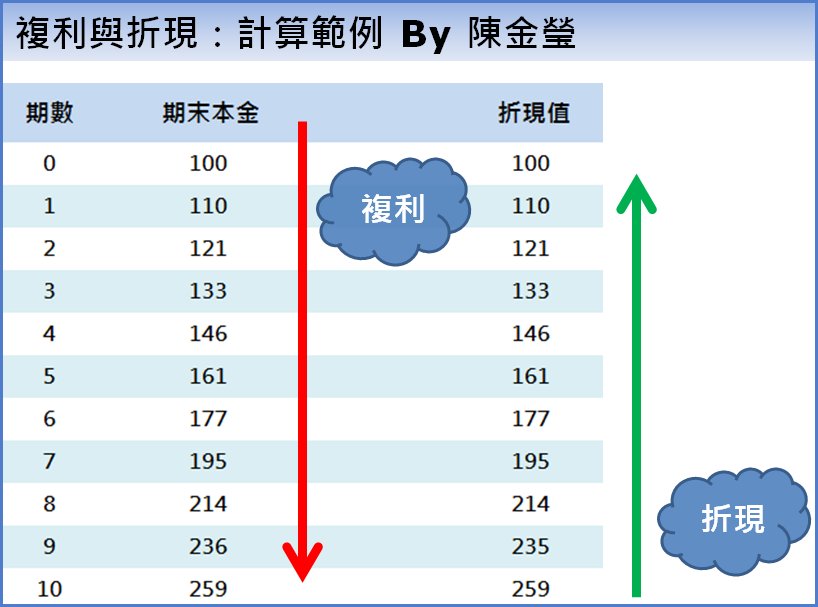
資料來源:陳金瑩
上面這個表
在 EXCEL 上的公式為 上期本金 × ( 1 + 報酬率 )
由於 100 萬滾一年,會變 110 萬
如果你很乖,沒把賺的錢拿出來花
而是繼續進場做投資
那麼到下一期,
這 10 萬還可以幫你多賺 10 × 0.1 = 1 萬
搭配上本來的 100 萬也能繼續賺 10 萬
所以到了第 2 期,
你的錢會變成 100 + 10 + 10 + 1 = 121 萬
滾了十年後,100 萬會變成 259 萬
複利效果為 259 – 100 – 100 × 0.1 × 10 = 59 萬!
而這「 10 年後」的 259 萬
如果你認為合理的折現率為 10% ( 視你對這項投資的風險高低而定 )
每年折回來 10% ( 公式為 上期本金 除以 ( 1 + 報酬率 ) )
整整折現 10 年,
也正好是 100 萬了!
結語
這篇文章,分享了幾個在數學上
對投資很有幫助的觀念與方法
本著「想做好投資,就該儘量相信客觀的事,壓抑主觀與情緒的判斷」
所以近年我花了很大的功夫
把以前學過的量化技巧
配合實際資料,把這些方法儘量都模組化
今天也正好抽空把這些心得
寫成這篇文章來分享
希望讀完以後,
您會覺得 ... 很有收穫喔!
《 本文作者簡介 》
陳金瑩 老師,畢業於台大經濟學研究所
歷任永豐金證券、安聯投信等大型投資機構
累積了 15 年豐富投資經驗
現為自由投資人
老師經常在網路上分享他的投資方法
並著有 凱旋投資術 這本經典著作
目的是幫助別人:
〝少走冤枉路、直接登堂入室穩穩賺!〞
在 FB 上有近 5 萬名粉絲
受到廣大網友的喜愛!
如果你喜歡這篇文章的話
歡迎幫老師的 粉絲專頁 按個讚 ↓↓
下次有新文章時 ~ 您才會優先收到喔!
本文作者 陳金瑩 的 Line 與 FB 專頁
《 順手「按」讚 ↓ 以後都能收到最新文章唷 》
本文受著作權保護,侵權需負法律責任!

 發表
發表


 我的網誌
我的網誌







